T1として5年生に算数の授業をすることになりました。
その、初日はこんな授業から始めました。
この記事が、現場のお役に立てたら幸いです。
数字はいくつ?
 Ri-せん
Ri-せん数字って いくつありますか?
すぐに挙手がありました。
ごめんね、いろんな人に聞いてみたいから、と言って
列指名していきます。
・分かりません。
・たくさん、あります。
そのうちに「無量大数」とか「無限」などというのが出てきて、
よく知っていますね、とほめていると、すっと手が挙がりました。



数字は、1から始まって9までで9個。0を入れると全部で10個です。
数字はたくさんある
首を傾げている子どもがいます。
数字は10個って?
そこで、発言を引き取って説明します。
T: 物の数を数えるとき、1から始めて1、2,3・・・と数えていきますね。
こういう数を自然数と言ってます。覚えなくいいですけど。
では・・・


1~9の数に0を加えたものを
何と言いますか?
即座に「整数」という言葉が返ってきました。 整数 – Google 検索



「整数」という言葉は、すでに習った学習用語です。
さて、
0と1~9の10個の数字を組み合わせると、
無限に数の大きさを表すことができます。
ですから、数字は10個と言っていいですか?・・・ダメですよね。
数字はたくさんあります、と言って板書していきます。


T: アラビア数字は、 「算用数字」とも言います。
T:「漢数字」 というのもありますし、 「ローマ数字」というのも見たことがあるでしょう。
T: 今では使われなくなった数字もあります。
そういう意味では、「数字はたくさんある」という答えになるでしょうか。
切ったら何本?
続けて、問題を出しました。
黒板を全て消して、
ぐねぐねとした1本の長い曲線を書きます。
子ども達は、何が始まるのだろうかと首を傾げて見ています。


T: 白い線は、1本の糸とします。
黄色い線ではさみで切っていくと、糸は、何本になるでしょうか?
子ども達は、
人差し指で空書きのようにしながら数えだしました。
列指名で言わせていくと、
16本,17本,18本,19本・・・といくつか出てきました。
数人に出て来てもらって数えてもらいます。
1本、2本、3本・・・と声を出しながらなぞっていきます。
糸は18本になるようです。
「一言どうぞ」と感想を求めると、
「大変でした」、「数え間違いしそうになった」と返ってきました。



もっと楽に数えられたらいいですよね。
それを知ったら、算数っていいなぁと思えてきますよ。
こんな方法は、どうでしょうか?
と言いながら糸が切れるところで印をしていきました。
その印に番号を付けていきます。
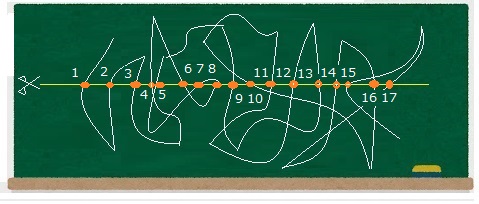

T: 17か所で切れました。ということは、糸は何本ですか?
C1: 17本です。
C2: え? 18本でしょう?
簡単にして考えてみる
事象を簡単にして考えてみる。
このアプローチの仕方が解決に有効な場合があります。



ややこしい問題は、簡単にして考えるといいですよ。
先生は、「簡単化」と呼んでいます。


T:糸を1回切ると、2本になります。2回切ると糸は3本になり、3回切ると4本になります。
C1:糸の本数は、切った回数に1多くなるんだ。
T: すばらしい!
この関係を式にしてみましょう。切った回数をロ。本数を〇とすると・・・?
C2: ロ+1=〇 です。
授業は、ここまで。
終了時間となってしまいました。
このあと、
本当にその式で答えが出るのか、
各自、図をノートに書いて確かめるようにするとよかったと思います。
この日の算数の「授業開き」にどんな感想を持ったのか、
書いてもらうつもりでした。
※ 数を当てる(予言マジック)と切ったら何本? という活動は、
2011年~2015年において研数学館が開催する「算数・数学講演会」にて
講師の先生方が話されていたものです。
お陰様で楽しい算数の「授業開き」ができました。
この場を借りて感謝申し上げます。
研数学館のセミナーはこちら 一般財団法人 研数学館 (kensu.or.jp)
