初任者研修の指導資料として過去に作成したものを今回リメイクし、
ブログ記事にして、発信することにしました。
現場の先生方の、授業づくりの参考になりましたら、幸いです。
T.T. (team teaching）のT1として５年生の算数授業をしていました。
以下は、「数直線を読む」授業の様子を内容としています。
１．数直線の「2.3ｍ」が指せない
５年生の算数授業、数直線を読むという活動の場面である。
まず作業指示をする。
Ri-せん数直線を読む、という勉強をしましょう。
ノートに10cmの直線を引きますよ。先生と一緒に書いていきましょう。
１cmごとに区切りを入れる。
左端は０。
右端には、23mと書くように指示する。
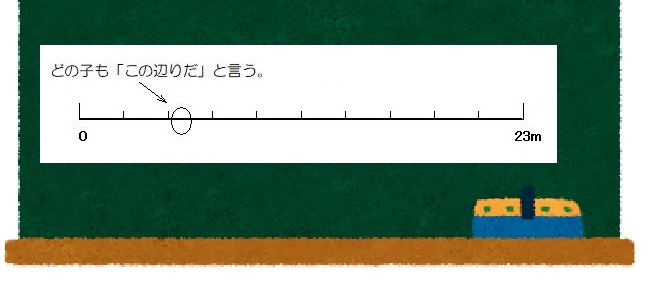
黒板にはこんな図（右図）が書き上がっている。
次に、列指名。
前に出てきた4,5人に指示する。
Ri-せん2.3m は どこでしょう。指してごらんなさない。
子ども達が席に戻ったところで、正解者の発表。
「正解者はゼロです。ざんねーん。」
自分こそは、と何人かが手を挙げ、チャレンジ。
どの子も「この辺りだ」と言う。
最初に指名された4,5人とどこが違うのだろうか、
微妙さに拘っているらしい。
学級の全員に問うてみても、同じ。みんな間違えている。（というか、見落としている。）
授業者の性格が問題になるが、
こんなときは、してやったりで、うれしくなってしまう質（たち）だ。
それが顔に出ないようにしながら尚、待てども一向に誰も気が付かない。
皆さんなら、こういう場合、どうするだろうか？
授業後の振り返り
どうするとよかったのか？
授業を振り返ることが大切だ。
次の発問が浮かんできた。
T：なぜ、そこを2.3mだ と思うのですか？
すると、子ども達はこんな反応をするだろう。
子ども2.3mは、２mと３mの間にあります。だからめもりの２と３の間です。
そこで一言。にこやかな表情をたたえながら・・・
Ri-せんなるほど！ そうすると、ここ（４めもり目）は４ｍになるね。
依然、当たり前だ、という顔。
じゃ、ここは５ｍだし、ここは・・・と続けるうちに子ども達の「あっ」という声がし出すはずだ。
子ども10めもり目は１０mじゃなくて23mになっている。
・・・ということは、23を10等分したところ、最初の目盛りが2.3mだ。
この数直線図は、教科書に載っている。
さりげなく描かれているから、アブナイ。
子ども達は、どっこい、読めていない（理解していない）。
関連記事
