授業は、「楽しい」が一番です。
フツーの教員にとって心がける授業づくりは、この一言に尽きます。
どうすれば授業が楽しくなるのか?
先生自身が、
テレビ番組のトークショーにおけるMCのようになって授業することです。
ひとり一人にスポットを当て
言葉を引き出し、その時間の目標を具現化していきます。
その過程を先生自らが楽しみ、子ども達も向上的に変容していく時間を楽しむ。
そんなイメージを私は持ちます。
授業で取組んだことをもとにシナリオの形にしてみました。
先生方のお役に立てたらなによりです。
※ 対象学年:4年生以上
教科:算数
内容:提示された事象を式に表す。
仕掛け
始まりのチャイムが鳴りました。
図を提示します。
T:●はいくつあるでしょうか。
すぐに5,6人の手が挙がります。
T:すごい! どーしてすぐに分かるの?
じゃ、答えを言ってみましょうか。さんハイ。
C:12個です。
式は3×4だよ。
4×3でもいいんじゃない、などという声がします。
T:●の数は12個です。正解です。 式もいいですねぇ。
じゃ、これはどうでしょう。


えっ、と言わせる
今度は、●がひし形状に並んでいます。
その数を問います。
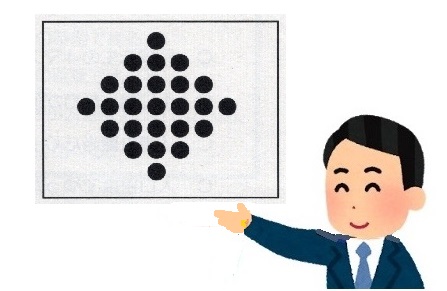

子どもたちは「え?」という表情になりました。
この反応を使わない手はありません。
T:なぜ、今「え?」となったのですか?
授業の冒頭に、子ども達が「え?」っとなる場面をつくります。
こうした仕掛けなしに授業を進めていくことはできません。
釣りで言えば、餌のようなもの。
喰いつかせるための手立てが必要となります。
これが、狙い通りに上手く作用していくかというと、
そうでもないことがありますから、苦労します。
(もちろん、考えるのが楽しみでもあります。)
自らの取組みを振り返り、日々授業改善に励まなくてはなりません。
反応を使う
図を提示した途端、なぜ「え?」となったのか。
前に座っている子どもから順番に聞いていきます。
挙手に頼ってはいけません。
ひとり一人にスポットを当てるように出番をつくります。活躍してほしいのです。


当てられた子どもが答えに窮するのは自然なことです。
上手く言えなくても、
気の利いたことを言えなくても
「大丈夫ですよ」
と気持ちに寄り添った言葉で包みます。
反応があるまでは、繰り返して投げかけます。
T:どうして「えっ?」ってなったのでしょうね。
言える子どもが出てきます。
C1:すぐには分からないから「えっ!」ってなりました。
C2:これは九九が使えそうもありません。
だから戸惑って「え?」となったと思います。
C3:計算ではムリだから、●の数を数えるしかないでしょ。
面倒なのでボクは「えーっ!」 です。
C4:えっ、ちょっと待っての「え!」です。
数えるコツがあるかもしれません。
聞きながら言葉の端々を書き留めておきました。
これを使います。





九九、計算は使えない、ということですが
計算ができれば、楽に●の数が求められますね。どーしましょうか。
子ども達は、ぽかんとしています。
計算で求めることはできない、そう思い込んでいるからでしょう。
最初の図に戻ります。



ちょっと戻りますよ。
初めの図は3×4で求めましたね。 この3や4って何ですか?
手が挙がります。 Aさん、どうぞ。



3はタテに並んだ●の数で、4は横の数です。
つまり、3個のかたまりが4つ分あるということで、3×4です。
期待通りの説明が返ってきました。よくぞ言ってくれました。
でも、ここは注意が必要です。
子ども達は話を聞いているようでいて、実は聞いていません。
分かっていないことがあります。
そこで、Aさんの発言を「見える化」してもらいます。
3×4とは何か。
図を使って話すよう、再び当てていきます。
くどいようですが、挙手に頼ってはいけません。


Bさんの番になって、左図のような説明がありました。
途端に、聞こえてきたのが「発見の感動詞」です。
あっ! うわっ! そうか!
何かがひらめいたようです。
授業中に発する子どもの「感動詞」は、楽しい授業のバロメーターです。
どんなことでしょうか。
共有していきます。



今、何かがひらめいた人がいますね。
どんなことか教えてください。ただし数字は言わないでくださいね。



Bさんが「見える化」してくれて、ある「かたまり」が見えました。
それなら、かけ算とたし算で求められそうです。



私は、かけ算とひき算です。



ぼくはたし算です。式が長くなっちゃいますけど。


これらの発言は、
小黒板(45×90cmの手作り黒板のこと) に書き留めておきます。
そして黒板の脇に掲示しておきます。



この図をどのように見ているか、分かりましたか?



「かたまり」としている●の数が、3人とも違うみたいです。



いくつかの「かたまり」に見て、後で計算している点は同じです。
クラス全員で
この段階で
子ども達は●の数を求める式を書けそうになっています。
各自で考えさせて自力解決の時間にする流れにできますが、
しません。
全員で一つの式をつくっていくことにします。



みんなで、式を考えてみましょう。
まず・・・●が何個で1つの「かたまり」と見たらいいでしょうか?
3人を前に出させます。
「かたまり」を指でなぞってもらいます。
3人とも同じでした。
●の個数が4個と3個の、2つの「かたまり」です。
チョークで線を引くと串団子のようになりました。
この図を言語化させます。
T:この図を説明してみましょう。
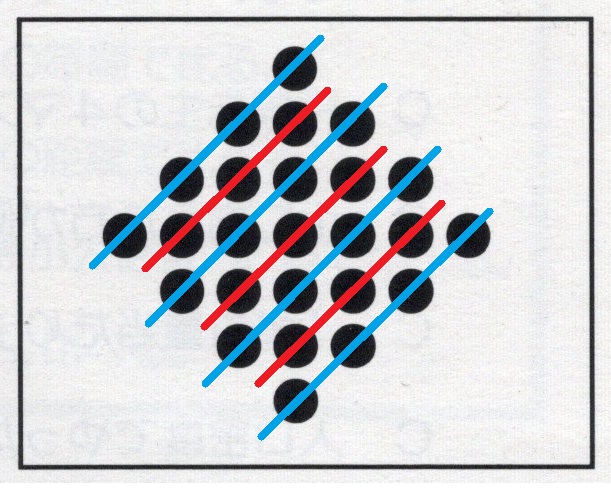

順番に指していくと
4個の「かたまり」が4つと、3個の「かたまり」が3つです、
と返ってきました。
あとは、簡単です。



計算で求める仕方が見えてきましたね。式と答えを書きましょう。
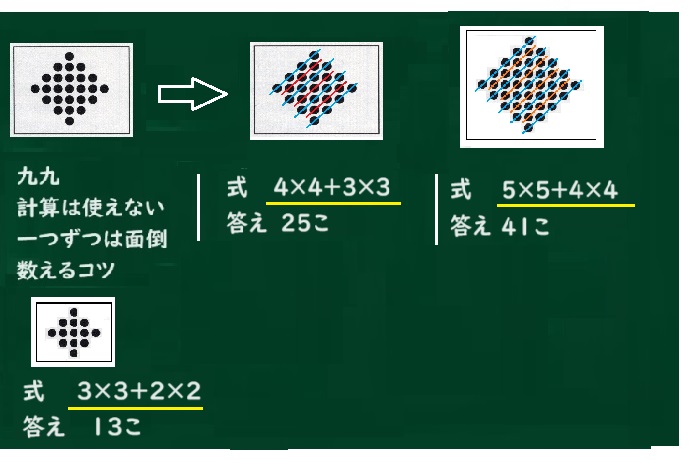
式は4×4+3×3で、答えは25こ。
赤鉛筆を持ち、
子ども達のノートを見ながらぐんぐん回っていきます。
よし!
と力強く言って丸をつけていくと子どもがにっこりとします。
その笑顔にうれしくなります。
半分回った辺りで、
お隣さんが困っていたらそっと教えてあげましょう、と投げかけます。


適用する
机間巡視からすばやく教卓に戻ります。
式と答えはCさんが書いておいてくれました。
最初の列を見ている際に板書を頼んでおいたのです。
次はどうなると思いますか、と言いつつ3枚目を提示します。
●の数が増えています。
T:これは、何こでしょう?
すぐに簡単じゃん、という声が返ってきました。
ノートに向かって鉛筆を走らせている子もいます。
式は、5×5+4×4。
答えは、25+16で41こです。
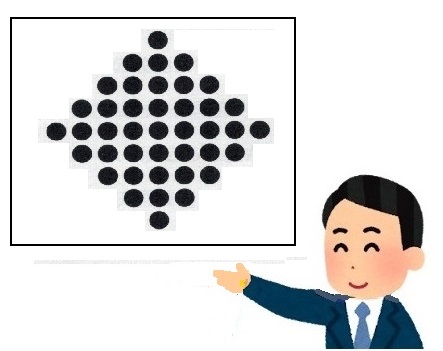

4枚目はこれです。
●の数が少なくなっています。
「さん、ハイ」で、式と答えを言わせます。
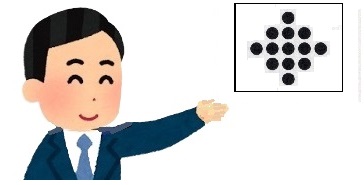

式 3×3+2×2
答え 13こ
同時に板書して、投げかけます。
T:ここまでしてきて、何か見えてきましたよね?
「うん」と言ってごらん。
しーん。
誰も「うん」と頷きません。
T:まだ見えてこないかぁ・・・では、ヒントを出しましょう。
今からチョークで線を引きます。3か所ですよ。どこに引くと思いますか?
漢字1文字のところですけどね。
C:漢字1文字って・・・?
一般化
3つの式に下線を入れました。
あっ! うわっ! そうか!
T:何か、気づいた?
C:3つの式は、同じです。
C:きまりがありそうです。
T:どういうこと?

手が挙がりました。



式の初めの数は
ひし形の一辺にある●の数で、「かたまり」はその数あります。



その内側は1こ少なくて、その「かたまり」はその数あります。
小黒板を取り出して3つの式を書き、
二人が言ったことが分かったか、問います。


T:これを見て、一言どうぞ。
C:ひし形の一辺の●の数が3,4,5・・・と増えています。
C:□×のところは、例えば●の数が6こなら、□に6。
7こなら、□に7を入れて計算します。
C:この式は、途中までしか書いてないけどね。



そう。式の続きを最後まで書いて見せにきてください。先着10名です。
持ってきたノートを見ると、右図のように書いてあります。
丸をつけ、小黒板を渡して
□=6のときの式と答えを書いてもらいます。
次の子どもには□=7のとき、
3番目には□=2のときを書いてもらいます。
書けたら黒板に立てかけてもらいます。







●の個数は、ほんとにこの数になるんでしょうか。
図を書いて確かめてみましょうか?



図を書いてもいいけど、
別な計算の仕方で、答えが同じになればいいと思います。
なるほど。
終末
他の求め方については、授業の初めで出ていました。
小黒板に書いておきました。
それを提示します。
T:「かけ算とひき算」で求める仕方はどうでしょう。
式が長くなるたし算は図をどう見ているのでしょうか。
これ以外にも数え方があるかもしれません。
「自学」で取組んでみては、と投げかけます。
授業は、終盤を迎えています。





ここまでの授業をみんなで振り返りましょう。
はい、全員起立!
思ったことをお隣さんと話し合ってください。
私の授業では、話し終えたら座っていいことになっています。
その話題に上ったことを言ってもらいます。
C:初めは計算できないと思っていたけど、□を使って簡単に求められました。
C:足し算だけで求めるのは、奇数を足していく式になるね。
C:かけ算とひき算で求めるって、どうするんだろう。気になる。
C:ほかにも●の数を求める式があるかもしれません。
自力解決型にすると・・・
●の数を求める式を各自でつくってみましょう。
こう投げかける授業にもできそうです。
様々な式が出てきます。
その後の授業は、こう流れます。
・全員で式の意味を共有する。
・比較検討する。
・まとめをする。
そのまとめとはどんなものか。
「みんな違って、みんないい」にはなりません。


比較検討を経ていちばんいい式が浮かび上がるはずです。
●の数が変化しても使えるもの、です。
その方向へ授業を引っ張っていくことになります。
授業における感動詞のいろいろ
感動詞は楽しい授業のバロメーター、と書きました。
以下に補足します。
1.発見(感動、驚き)の感動詞 ・・・ あっ! うわ! そうか!
2.否定(意外性)を示す感動詞 ・・・ えっ! あれ? はっ?
3.納得の感動詞 ・・・ うん ふうーん へー ほう なるほど!
4.同意の感動詞 ・・・ そうそう! やっぱり!
5.疑問を示す感動詞 ・・・ あれ? これ? そう? どうして? どこ?
6.非難を示す感動詞 ・・・ はぁ? んー? あー? えー?
7.補足を促す感動詞 ・・・ だったら~ じゃあ それなら~ だって
参考 山本良和著「算数授業のつくり方」 東洋館出版社 2013年

