「一筆書き」の図形から「きまり」を見出す授業をしました。
先生方の授業づくりのお役に立てたら幸いです。
※以下の記事は、5年生に行った授業をもとにしています。
効率よく授業を進めるためには、準備が必要です。
授業のはじまり
チャイムが鳴りました。
用意しておいたカードを1枚ずつ貼っていきます。
子ども達は、何が始まるのだろうと黒板を見ています。
6枚貼り終えて投げかけます。
※カードは25cmくらいの大きさでつくります。
裏にはマグネットがついています。





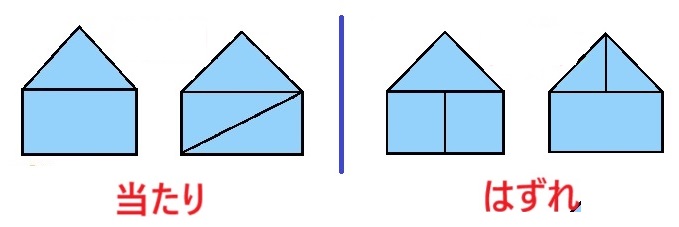
今日の授業は、
「当たり・はずれ」ゲームから始めます。
6人を指名します。
任意にカードを1枚選ばせたら、
そのカードが「当たり」か「はずれ」かを言ってもらいます。
どうして
「当たり(はずれ)」と思ったのか。
理由は問いません。直感でOKです。


直後に、判定します。
T:はい、お見事です。これは「当たり」のカードでした。
T:あー、残念。これは「はずれ」なんですよ。ドンマイ!
はい、次の人! ・・・という風に。
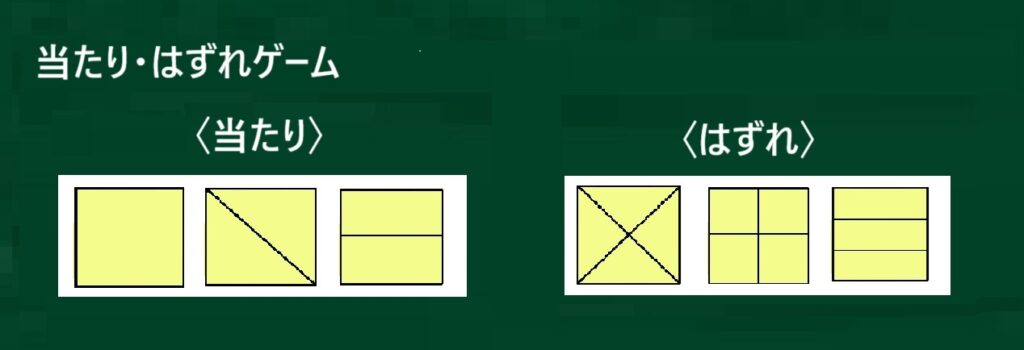
6枚の「当たり・はずれ」が分かりました。
カードは2つに分けて並べます。
そこで問います。
T:どうなっていると「はずれ」なのでしょう?

すぐに手が挙がりました。



中に2本の線があると、「はずれ」です。
どういうこと?
全体に向かって問い返します。
子ども達は、意外と聞いていません。あるいは、分かっていません。
それで別な子どもに答えさせます。
指名された子どもが前に出てきて説明し、「中の直線2本」をなぞってくれました。
なるほど、「はずれ」はみんなそのようになっています。
全員が納得。
一方の「当たり」の図形には中に直線がないか1本のみになっています。
では、これはどうでしょう?
「当たり」か「はずれ」か。
反証
新たに図を提示し、座席の順に当てていきます。


C1:はずれです。
C2:はずれです。 ・・・以下数人も同様。
T:あれれ、みんな「はずれ」ですね。
なぜそう思ったのですか?
C3:中に直線が2本あるから、です。
T:なるほどねー。
先ほどの、見つけ出したきまりを基にして考えたのですね。こういうのを類推といいますよ。
スイスイじゃないよ。るいすい。
前がそうだったから、これもそうだろうと考える。いいですねぇ。
・・・でも、残念。これは「当たり」のカードでした。
え、どういうこと?
子ども達は、ぽかんとしました。
テンポよく進める
間髪を入れずに、新たなカードを取り出し、フラッシュして見せていきます。



「当たり」か「はずれ」か言いましょう。 直感ではい、どうぞ。

① C’s:当たり! ※ C’s・・・子ども達の略
T:正解です。「当たり」でした。
② C’s:当たり!
T:正解。「当たり」です。
③ C’s:はずれ!
T:ざんねーん。これも「当たり」なんです。
C’s:えーっ! 中に2本直線があるじゃん。「はずれ」でしょう。
笑顔で返して、続けます。

④ C’s:当たり! (はずれ!の声も)
T:「当たり」と言った人、ざんねーん。これは「はずれ」でーす。
⑤ C’s:はずれ!
T:お見事。これは「はずれ」です。
⑥ C’s:あたり!
T:・・・と思うでしょ。 「はずれ」なんですよ、これが。
C’s:えーっ! どーなってんの?
混乱して来ました。しめしめ、です。
※この時点で黒板は、右のようになっています。



何か見えてきましたか?



何が「当たり」で「はずれ」か
ぜんぜん分からなくなりました。
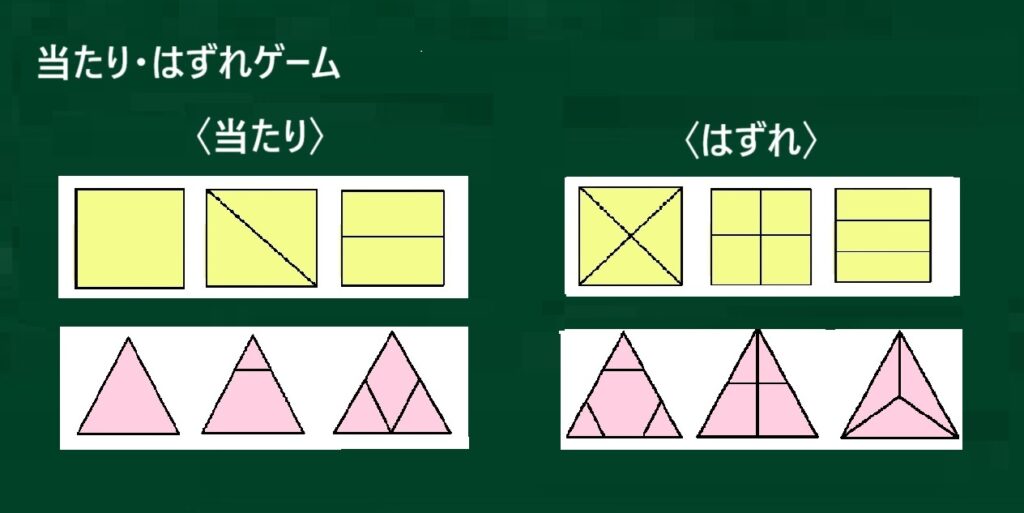

教室が、困惑の色に染まり空気が冷えていくのを感じつつ、にこやかに続けます。
「当たり」とは?



これを見れば、気づく人がいると思いますよ。家の形のカードです。
T:左側は「当たり」で、右は「はずれ」です。
T:では、これはどっちでしょう。



C1:あ! この形は見たことあるよ。なんだっけ。
C2:それは「当たり」のような気がします。
T :そのとおり。「当たり」です。
「当たり」のカードって何だと思いますか?
数人がひらめいたようです。手が挙がりました。



ひょっとして、それは4文字の言葉ですか?



そうです。数字から始まって「き」で終わる言葉です。



分かった。 「一筆書き」でしょ。
何人かが人差し指を立てて、空書きを始めました。
黒板に貼ってあるのが「一筆書き」できるのか確かめ出しました。
用語をおさえる
まだ確認中の子ども達がいますが、授業を前へ進めます。
「言葉(用語)」をおさえます。



「一筆書き」って、何ですか? お隣さんに説明してみましょう。
ペア学習です。
これをするときは、立たせて行います。
じゃんけんで負けた方が説明する、というふうにすると真剣になります。
このルールでの話し合いは子ども達は初めてではありません。
説明が終わったら座ってよいことにしてあります。
2割ほどが座ったら、共通理解をはかります。
全員が座るのを待っていてはいけません。ダレます。
なかなか座れないのは説明しづらいからです。
早めに座った何人かを指名し、言わせます。
説明の仕方が少しずつ異なるので整理し、それをノートに書かせました。
「一筆書き」・・・同じところを2回以上通らないでその形を書くこと。
意味を押さえたら「一筆書き」でできるのか実際に確認します。
座席の順に当てて、前へ出させなぞらせます。
できません。
指を行きつ戻りつさせています。
その様子を見ているうちに気づきます。
「一筆書き」を始める点があることを。
そこに印をつけさせます。
カラーマグネット(赤)を置かせました。
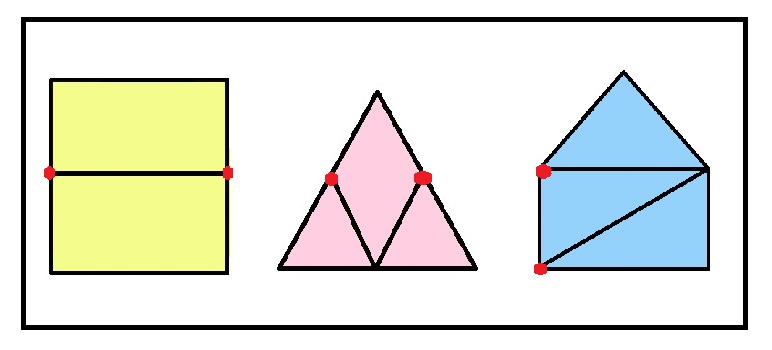

始点に印をつけると
その印に注目させます。



印をしたところを見ていて、何か気が付くことがありませんか。



どの形もそこから3本の直線が出ています。



印のないところは、直線が2本になっているよ。
4本出ているところもある。
印をつけた点の呼び方を決めます。
名前を付けておくと以後の説明がしやすくなります。
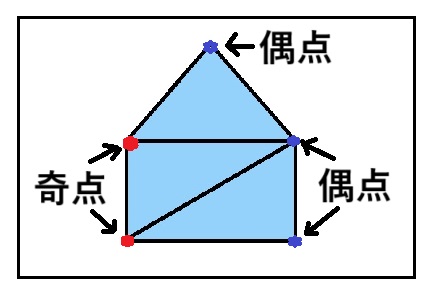

T:直線が3本出ている所は、3が奇数なので「奇点」。
2本、4本出ている所は、2や4が偶数なので「偶点」と呼びましょう。
この言葉をさっそく使います。
T:「一筆書き」は、「奇点」から始めます。
「偶点」から始めると一筆で書けません。・・・ホラね。
各自でも確かめるよう、30秒ほど与えます。
「奇点」の数
今度は、「奇点」の数に注目させます。



黄色で囲った2つの図形を見ましょう。
「奇点」はいくつありますか?



え?
「奇点」というのは、直線が奇数の数出ていることだから、これには「奇点」はありません。ゼロです。



つまり、「奇点」がない図形は
「一筆書き」ができる、ということね。
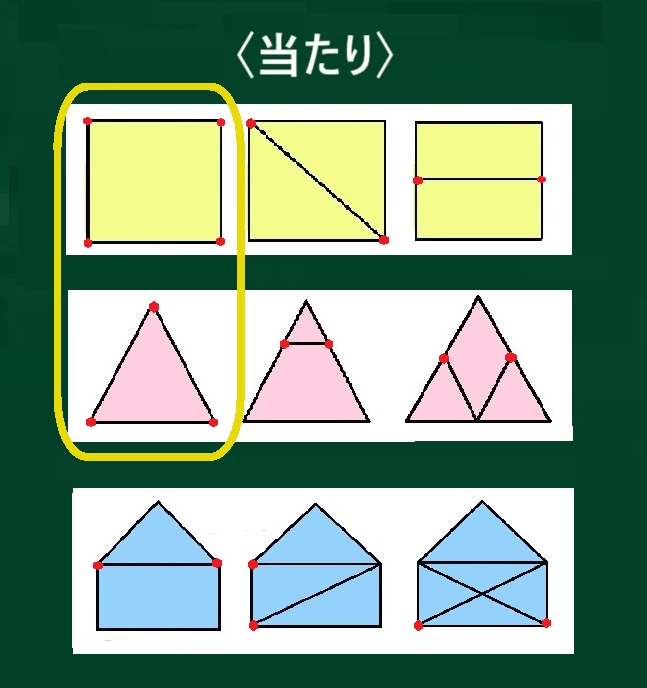

うまくまとめてくれました。そのことを確認します。



これは「一筆書き」できるでしょうか?


C4:この形は、全部「偶点」です。
C5:ということは「奇点」がゼロだから、一筆で書けるはずです。
T :ホントかなぁ。 では、ノートに書いてみましょう。
「奇点」がない。
このフレーズを黒板のはじに書き留めておきます。
「一筆書き」のきまり
次は、残った方の図形を囲みます。



こちらも「奇点」の数を見てみましょう。あることに気づきますよね?
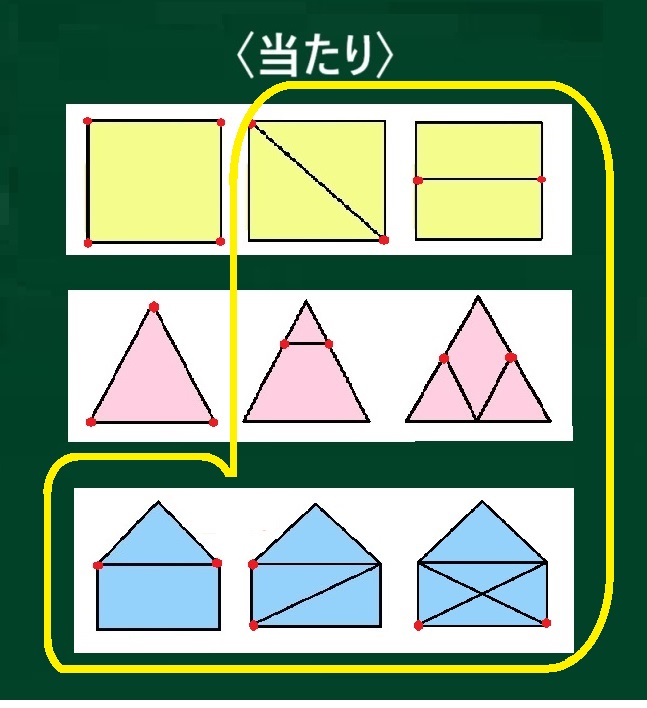

C6:どれも「奇点」は2こしかありません。
C7:ホントだ。
C8:「一筆書き」ができる形は、「奇点」が2つ、ということかな。
このフレーズも黒板のはじに書き留めておきます。
C9:「奇点」が4つだと一筆でかけないのかな。
T :C9さん、とてもすばらしい思い付きです。
〇〇だったらどうか、というのは条件を変えて考えるということです。
誰かがそう言うのではないかと思って、用意しておきましたよ。
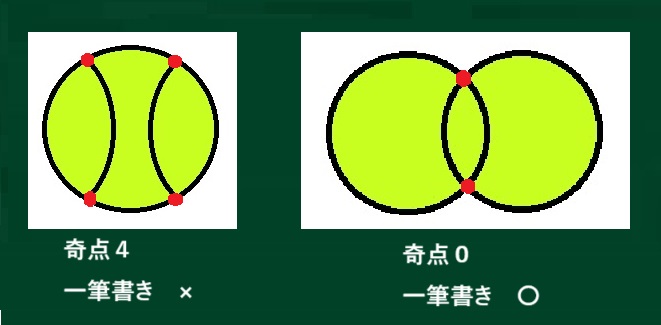
球形の形を出します。



「奇点」を見てみましょう。 「一筆書き」のできるのはどっちかな?
C2:野球ボールみたいな形の「奇点」は4こ。
だから「一筆書き」はできないんじゃないかな。
C3:できないよ。今やってみました。
「奇点」4こはやっぱりダメです。
C4:右の方は「奇点」がありません。
だから「一筆書き」ができると思います。
C5:これは簡単に「一筆書き」できたよ!

T :今日は、「一筆書き」の形について見てきました。
どんなことが分かりましたか、ノートに書きましょう。箇条書きで3行になるといいですね。
机間巡視します。
数人に板書させます。


オイラーの話
時計を見ると、授業終了まであと5分です。
画像を映します。
お話です。


T:スイスのお金で、10フラン紙幣です。現在は使われていません。
描かれている人物はオイラーといって300年くらい前の人です。
大変有名な数学者です。
イラストを映します。
T:ケーニヒスベルクという町に橋が7つ架かっていました。
この7つの橋を2度通らずに全て渡ってもとに戻れるか、と町の人が言いました。
T:2度通ってはいけないというのは「一筆書き」のことです。
オイラーは簡単な図にして考えました。
C:先生がよく話している「簡単化」ですね。
T:そうです。簡単にするとこうなりました。
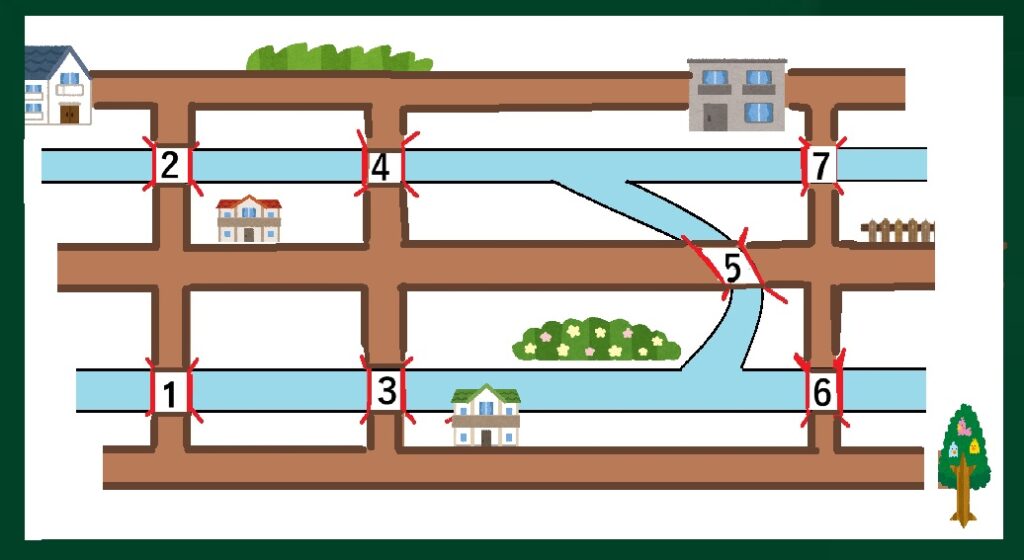

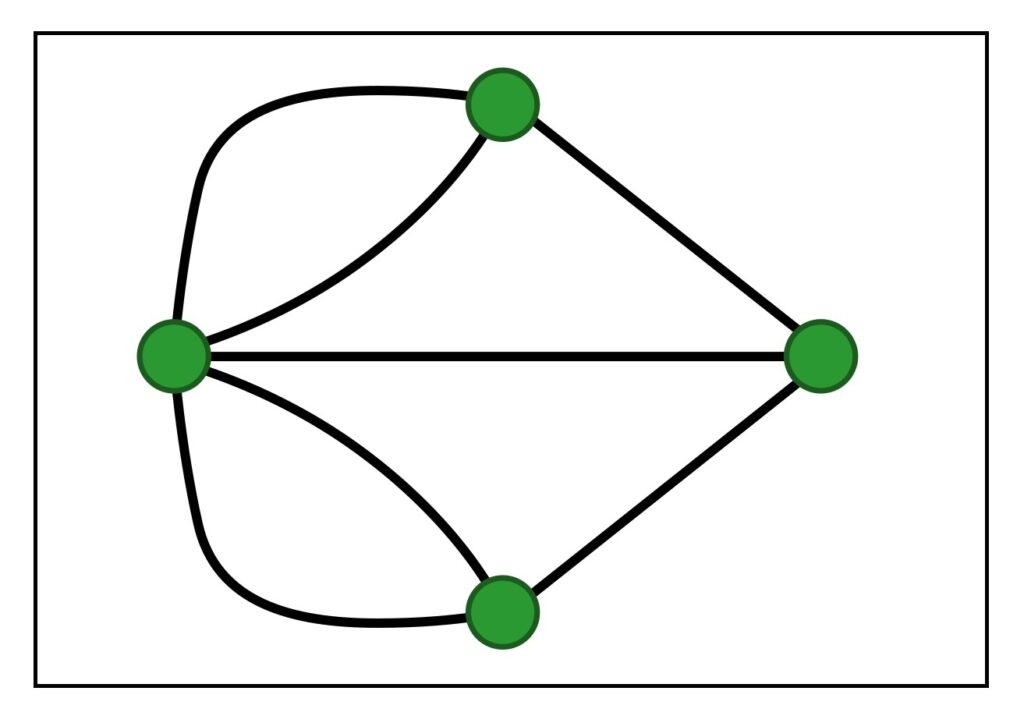
図を映します。



この形が「一筆書き」できるか、何に目をつければいいですか?
C1:「奇点」の数です。
C2:「奇点」が2つか、ゼロなら「一筆書き」ができます。
C2:この図形は「奇点」が4つです。だから「できない」かも。
T:そう、「一筆書き」できません。
ということは、7つの橋を2度渡らずに元にもどることは
できない、ということになります。
オイラーはこのことを証拠を挙げて明らかにしました。
オイラーは数学や物理を研究し、人類史上最多の論文を書いた人とも
言われています。

適用



それでは最後に問題です。
この形は、どうしたら「一筆書き」できるでしょうか。
提示されたものから1つ選んでノートに写します。
次に「一筆書き」でなぞらせます。


クリア出来たら次の形へとチャレンジさせます。



さて、皆さんは今日の授業についてどんな感想を持ちましたか?
感想を一言書かせて授業を閉じます。

