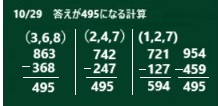
答えが必ず「495」になります。
そんな「引き算の授業」をしてみてはいかがでしょう。
繰り下がりのある筆算の練習にもなります。
※この計算については研数学館が開催する「算数・数学講演会」で知りました。
2011年~2015年の頃だったと思います。
毎回、算数・数学の授業づくりに大変役立つお話をいただきました。
この場をお借りして感謝申し上げます。
研数学館のセミナーはこちら 一般財団法人 研数学館 (kensu.or.jp)
概要
答えが「495」になる計算は以下のようにします。
1.0~9までの10この数字から3つ選ぶ。
2.その数字を使って、最も大きい数と最も小さい数をつくる。(3位数)
※0を選ぶと2位数。後述)
3.引き算をする。
式は2でつくった(最も大きい数)-(最も小さい数)。
答えは必ず495になります。例えば・・・
10この数字から、(3,6,8)を選んだとします。
最も大きい3位数は(863)。最も小さい数は(368)です。
引き算は、863-368。
答えは、495になりました。


たまたまでしょうか。
数字を選び直して(2、4、7)でやってみます。
最も大きい数は(742)。最も小さい数は(247)。
742-247 をします。
やはり、495 になりました。
これも、たまたまでしょうか。


以下は、授業シナリオです。
※5年生での実践をもとにしています。
授業シナリオ
休み時間のうちに板書しておきます。
日付、及び今日の授業のタイトル(495になる計算)です。
それを見て、子ども達が席に着き始めました。
授業開始。
T:答えが必ず「495」になる引き算があります。
子ども達は、どういうこと? といいたげな顔をしています。
続けます。
T:まず、0~9の数字の中から3つ選びます。
例えば・・・3,6,8 を選んだとしましょう。



この3つの数字を並べると3桁の数になりますね。
その中で、一番大きい数をノートに書いてごらんなさい。
ノート指導は大切です。
日付とタイトルを書いた後、どのように書くのか指示します。 ⇒右図
一番大きい数を「863」と書いているでしょうか。
隣同士で確かめ合うようにします。ペア学習です。
次に書くのは、最も小さい数。
「368」の下に横線を定規で引かせたら、
さあ引き算をしてみましょう、と投げかけます。


ホントだ。
495になった、と驚いている子どもに交じって、こんな反応があります。



先生、「495」になったのはたまたまでしょ。
そうかもしれません。
数字を変えて(2、4、7)でやってみます。
隣のスペースに自分でやるように指示します。
さーっと子ども達のノートを見ていきます。
答えの正誤をチェック。
指示通りにきれいに書いてるノートはほめます。
巡視中、つぶやきが耳に入ってきます。
あれ?
やっぱり495だ。


キツネにつままれたようになっている子ども達。
このようになるわけをおさえておきましょう。
495になる仕組み
一旦、授業シナリオから離れます。
引き算の答えが495になる仕組みについて、です。
任意に選んだ数字を大きい順にA、B、Cとします。(但、C≠0)
それによってできる最大の3位数は、① 100A + 10B + C
最小は、② 100C + 10B + A と表せます。
引き算は、① - ②。
整理すると、99(AーC)となります。
AーC=5 のとき、
つまり、選んだ数字の最大と最小の差が5だと、
引き算の答えは、その99倍の「495」になります。


(3,6,8)と(2、4、7)を例に挙げたのは、
選んだ数字の差がどちらも5なので、口上のとおりになるからです。
子ども達が「495になったのは、たまたま」というのは、そのとおりで、
AーC ≠5 の場合は、495にはなりません。
その場合はどうするか?
話を授業シナリオにもどします。
495にならない時は…
なんか、怪しいなぁ・・・
そんな声のする方へ目をやると、手が挙がりました。



先生は、たくらんでると思います。
ぼくが数字を選んでいいですか。(1,2,7)でやってみてください。
「たくらんでいる」とは、おだやかではないですね。
でも、数字を変えてみたら、というのは授業を深める発言です。大いにほめます。
さっそく、やってみます。
式は721 - 127 答えは594。
確かに「495」にはなりません。
そんなときは、
その「594」を使って最大と最小の数をつくります。
つまり、954 と 459。
式 954ー 459
答えは、495になりました。

「 495」 にならないときは、その答えの数字を使って最大と最小の数をつくる。
進め方について付け足しの話をしていると、首を傾げている子がいました。



〇〇さん、何か疑問に思うことが浮かんでいるのかな?



数字は0を選んでもいいんでしたよね。
例えば、0、1、7にしたらどうなるのかなって・・・。
0を選んだ場合
よくぞ気が付いてくれました。
その発言で授業が更に前へ進みます。いっぱいほめます。



じゃあ、(0、1、7)でやってみましょう。
自分で確かめたい人はどうぞ、にします。
すぐにあれ? と戸惑う声がしました。
最大の数の「710」はいいとして、最小は「017」でいいのか?
何かヘンだな、そんな空気。



もう一つの「017」。 これ、どうしましょう。


賢い子がいるものです。手がすっと挙がりました。



「017」の「0」は百の位を0と見て、17として計算すれば?
なるほど、なるほど。それでいこう。
筆算再開。・・・答えはやはり「495」になりました。



今のところみんな「495」になってますが、
そうならない場合もあるんじゃないか、と思っている人いるでしょう?
投げ掛けてみると、ぱらぱらと手が挙がります。
これは確かめないといけません。
この数字を選べば「495」にはならないかもしれない。
いろいろと試してみることにします。
繰り下がりのある引き算の練習にもなります。
「終わり」は示しておきます。
とりあえず3回したら鉛筆を置いてもいいことにしました。


共有
頃合いをみて「個」の活動から「全体」に戻します。
どんな数字を選んでも最後は「495」になる。
その検証をします。
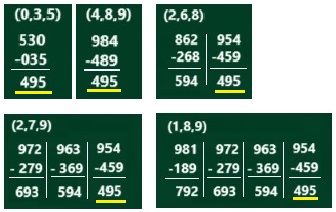
指名された子どもが書いた筆算で黒板はいっぱいになっています。
※右の写真はイメージです。


数字を3つ選ぶ組み合わせはたくさんあります。
(0、3、5)、(4、8、9)、(2、6、8)・・・
同じものは出ていないようにしてあります。
では、共有していきましょう。



黒板を見て一言、言いましょう。

座席の順番で当てていきます。「挙手」に頼ってはいけません。
いずれ自分の番が回ってきますから子ども達は考えます。
C1:答えが全部「495」になっています。
確かにそう。例外は今のところないようです。
C2:どういう仕組みでそうなるのか、不思議です。
そう、不思議だよね。 共感してそこでとどめておきます。
C3:筆算が1回で「495」になるのは、数字の差が5になっているときです。
ここは立ち止まります。



今すごい発見を言ってくれたんですけど、分かりましたか?
詳しい説明を求めると、
(0、3、5)は、選んだ数字の最大と最小の差が5になっている。(4、8、9)も同じ。
その場合、答えが「495」になっている、と言いました。
T:よくそこに気が付きましたね。すごいなぁ。
発表が続きます。



答えが「693」になると、
「495」になるまでは同じ筆算になっていきます。
どういうことか。
前に出て来てその部分を指してくれました。
(1、8、9)の2つ目以降の筆算は、(2、7、9)の筆算と同じになっています。
あっ!
どうしたの、と聞いてみると「すごい発見をしちゃった」と言います。
(1、8、9)の筆算の答えを横に見ていくと・・・



「9」が浮かんできました。
792⇒693⇒594⇒495は、9ずつ減っているんです。
すると、
(0、3、9)で筆算をした子どもの手が挙がりました。
初めの引き算が「891」。
次は「792」だからやっぱり9ずつ減っていると言います。
「9」は、この計算の仕組みに関係する数のようです。
ちなみに、
891、792、693、594、495は全て9の倍数です。
9で割り切れる、という発言はありませんでした。
反論が出た場面もありました。



筆算の回数が多いものは、選んだ数の差が大きい場合です。
すると、



(0、1、2)でやってみたら筆算は5回でした。差は2です。
だから、差の大きさと筆算の回数は関係がないと思います。
(1、2、3)の場合も同様で、
差が2なのに筆算は5回もしてやっと「495」になったと言います。
差の大きさと筆算の回数にはどんな関係があるのでしょうか。
選んだ数の差と筆算の回数
授業では深入りを避けます。
興味がある人は、家で調べるよう投げかけました。
ここでは、教材研究としておさえておきます。
10この数字から3つ選び、大きい順に(A、B、C)とします。
AとCの差を「n」としたとき、C=Aーnとなって(A、B、C)は【A、B、(Aーn)】と表せます。
これを使って3位数をつくると、
① 最大の数 100A + 10B + (Aーn)
② 最小の数 100(Aーn) + 10B + A となります。
引き算は ① ー ②
その答えは、「99n」です。
すなわち、最初に行う引き算の答えは、選んだ数字の差の99倍になります。
答えが「495」になるまでの筆算の回数を以下に整理してみます。
※ nは、選んだ3つの数字の最大と最小の差です。
| 筆算の回数 | 初めの筆算 | 2回目の筆算 | 3回目の筆算 | 4回目の筆算 | 5回目の筆算 |
| 1回 | n=5のとき 答え 495 | 無 | |||
| 2回 | n=6のとき 答え 594 | 954-459 答え 495 | 無 | ||
| 3回 | n=7のとき 答え 693 | 963ー369 答え 594 | 954-459 答え 495 | 無 | |
| n=4のとき 答え 396 | 同上 | 同上 | 無 | ||
| 4回 | n=3のとき 答え 297 | 972ー279 答え 693 | 963ー369 答え 594 | 954-459 答え 495 | 無 |
| n=8のとき 答え 792 | 同上 | 同上 | 同上 | 無 | |
| 5回 | n=2のとき 答え 198 | 981ー189 答え 792 | 972ー279 答え 693 | 963ー369 答え 594 | 954-459 答え 495 |
| n=9のとき 答え 891 | 同上 | 同上 | 同上 | 同上 |
筆算が5回になるのは、選んだ数字の差が2と9のとき。
筆算が4回になるのは、3と8のとき。
でした。
数字の差が大きいと筆算の回数が多くなる、とは一概にいえないことが分かります。
授業シナリオに戻ります。
終末
今日の授業について感想を言ってもらいました。
この活動から発展するような課題が出ることを期待してのことですが、難しいものです。
そこで、こちらからタネを蒔くことにします。



「9」は不思議な数だなぁ、と先生はときどき思います。
続けます。
T:実は、答えが必ず「9」になる引き算があります。
今度は、数字を2つ選びます。
2桁の数をつくって引き算するんです。
(いくつかを例示)
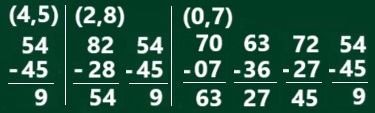

もう一つ。
今度は数字を4つ選んで4桁の数をつくります。



引き算を続けていくと・・最後は必ず□□□□になります。
その数は何でしょう。 ※
その数は「9」で割り切れます。
「9」って、不思議な数ですねー。苦労(9ろう)と思わないでみなさん、調べてみましょう。
・・・と投げかけて授業を閉じます。
※その数は6174です。
関連記事