授業の始め方は、様々です。
天気の話とか、世間話とか、
授業につながっていかない話から始まったり、
「はい、16ページを開いて!」などという事務処理的な始まりをよく目にしてきましたが、
それらは論外です。
最初が肝心。
面白くなさそう、などと思われたら、
TVを見ている場合なら忽ちチャンネルを変えられてしまいます。
わくわくさせる。
引き付ける。視線を集める。
えっ? と思わせる。なぜだろうと考えさせる。
答えざるを得ない状態をつくる。瞬時に考え、立場を決めさせる。
そういうベクトル(方向と量)をもったはじまり方をすべきです。


授業とはある意味、「強制」です。
内容は決まっています。指導する学年も時期も決められています。
それらを一定期間のうちに修得させねばなりません。
子ども達は、つまらないからといって、チャンネルを変えるわけにはいきませんから
仕方なくやるか、終わるまで死んだふりをしてやり過ごそうとします。
なんとかしないといけません。


秒殺という言葉がありますが、
数十秒のうちに子ども達を授業者の手の平に載せる、
そんな授業の始まり方ができたら、といろいろ試行してきました。
一旦載せたら、
そこから一人もこぼさないように手を打っていきます。
まずは、始まりが大事です。
授業の始め方は様々あります。
その一つとして、「ものの提示」から始めるというのがあります。
何も言葉を発せず、ものを出す。
子ども達が、何だろうと思ったところで投げかける。
そういう始め方があります。
以下は、5年生の算数「体積」の授業についての取組みを紹介します。
少しでも、現場の先生方のお役に立てたら幸いです。
面積から始める
授業時間になりました。
黙って、二つの図形を黒板に貼ります。
正方形と長方形です。
一呼吸おいて、投げかけます。



どっちが広いでしょう。
子ども達の反応は、3つに分かれました。
青い方だ。
いいや、黄色い方だ。
どちらも面積は同じかも。
すると、
ある子どもが、「重ねていい?」と聞いてきました。
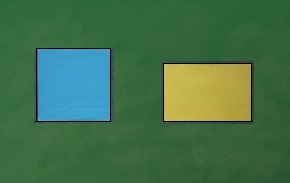

対象のものに働きかけてみる、その発想を大いにほめます。
重ねる、とはどのようにするのか。前に出て来てやってもらいます。
なるほど、そう重ねるのか。
おお、やっぱり同じですよね、ととぼけると
はみ出ている短冊の部分が違うと言います。
そう言うと思ってね、用意しておきました、と
短冊の部分を取り出し、並べてみると
青色の方が、大きい!
となります。
では、どのくらい大きいのでしょうか。

すると、長さを測ればいい、と子ども達。
あっさりと答えてしまいます。



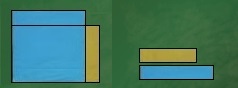
実は、1つは正方形で1辺が5cm。
もう1つは長方形で縦4cm、横6cmで作ってありました。
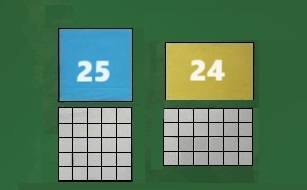
そして、マス目になった紙を貼ります。
マスの数は25と24。
だから正方形が広い。
そこで、問います。



広さを比べるときは、どう表したらいいでしょう?
「1㎠ がいくつ分で表します。」
などと子どもは絶対に言ってくれません。




「たて×横」で求めます。
その答えに面積の単位を付けて表せばいいんじゃないの。
そこで問い返します。
なぜ「たて×横」という計算をするのでしょうか?
なぜ「たて×横」か
すでに学習していますが、説明が出来る子どもはいません。
そこで、おさらいです。



長方形の面積の式、4×6はどういう意味でしょうか?
1辺が1cmの正方形の個数を求めているのですよね。
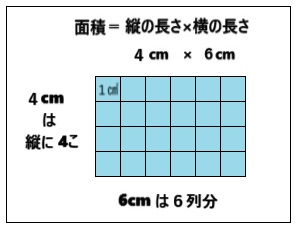

縦と横の長さをかけているのは、
1㎠の正方形を単位として、その個数を求めているのでした。
縦の長さ4㎝は4こ。横の長さ6cmはそれが6列あるということ。
つまり、
辺の長さと1㎠の個数とは数が同じだから
長さを測って計算すれば、面積が求められるというわけ・・・
だったよね。
面積を求める公式の意味をおさらいしました。
「単位がいくつ分で表す。」は、長さも同じ。
5㎝は、単位の1㎝が5つ分だし、3mは、単位の1mが3つ分です。
重さも液体のかさも同じです。
「単位とするものがいくつ分」は、
算数授業における合言葉にしておくといいかもしれません。
新しい単位が要る!
ここまで来て、やっと5年生の中身に入ることができます。
図を提示します。
ここで「新しい単位がいる」と言わせたいわけです。
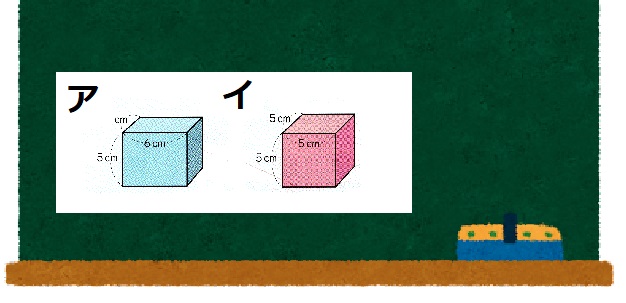

T:どっちが大きいでしょう。
子ども達は、「同じ」と言います。
理由がおもしろい。(失念)
続いての投げかけも同じ。
かさ(体積)は、どのように表したらいいのでしょう。
発言がなければ、誘導します。
T:合言葉はなんだっけ?
C:新しい単位が必要、ということ?
T:それは、どんな形をしている?
「サイコロみたいな形の個数で比べる」という発言が返ってきました。



そのサイコロの大きさを、手でやってみてください。
もちろん、
1辺が1cmの立方体です。1㎤という単位を教えます。
関連記事


