棒で正方形をつくって、横につなげていきます。
正方形がｎ個のとき、棒は何本か？
5年生に行った授業を元に、シナリオにしてみました。
現場の先生方のお役に立てたら幸いです。
授業の準備
① 四つ切の画用紙を1枚用意します。
横長になるように2枚にカットし、つなげて短冊状にします。
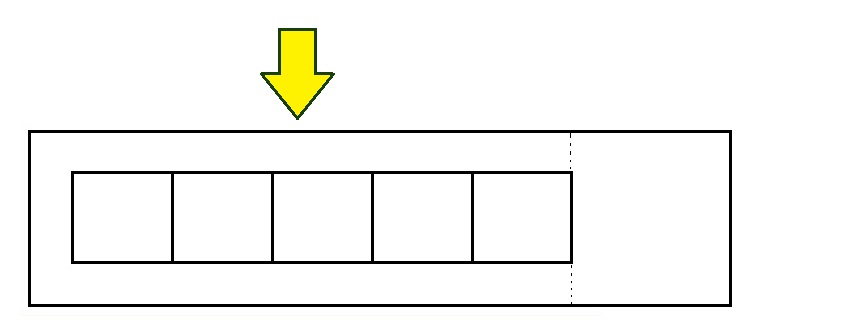
その画用紙に正方形を７つ書きます。（右図）
正方形が５つになるように、短冊の右端を折り返します。
２つ隠すのです。
その意図は後述します。
② 短冊黒板を用意します。（学校備品）
子ども達が考えた式を書くのに使います。
10～15枚くらいあるといいです。
③ 板書を決めておきます。
授業終了時の黒板を
ノートに書き、シミュレーションしておきます。
授業のはじまり
ちょっとしか見せないよ。
おもむろにそう言ってマスの書かれた画用紙をちらりと見せ、すぐに伏せてしまいます。
T：何が書いてあったでしょう。
C：えっ？
C：マス目がいくつか書いてあったような・・・。
もう一度見せますね、と言って問題を出します。
T：ここに書かれている棒は、何本でしょう。
たぶん、当たらないと思いますけど・・・。
さっそく数え始めた子ども達。
人差し指で１，２，３，４と空書きのようにやり出しました。
５秒ほどで伏せてしまいます。
全員が数え終わるのを待ちません。
C：えー、早すぎる。数えられなかったー。
C：16本です。
C：15本じゃないの？
そこで投げかけます。
Ri-せんいま、棒の本数をどのように数えましたか？
即座に手が挙がりました。
説明する
今、手を挙げている人達。どうぞ。
みんなの前で、
どのように本数を数えたか、実際にやってもらいました。
１、２、３、４と言いながら指示棒でマスをなぞるよう指示します。
子ども達は誰からやるかじゃんけんを始めました。
なかなか自治的です。
トップバッターの子どもは、横棒の数の次に縦棒を数える仕方でした。
１から16までの16本です。
２番目は、
上と下の棒の数が同じで5本ずつ、縦は6本。合わせて16本と数えました。
なるほど、なるほど。
出番を待っていた子どもは、言われてしまったようです。
「同じです」と言って席に戻っていきました。
Ri-せん16本のようですね。それ以外の数え方はありますか？
タケノコのようにあちこちから手が挙がりました。
順番に指して、同じように黒板でやってもらいます。
すると、このような説明がありました。
棒2本でL字の形にすると５つあるでしょ。残りをたして16本です。
ぼくは、コの字にして数えて16本になりました。
まだ手が挙がっていますが、一旦下ろさせます。
Ri-せんその数え方を、式に表せますか？
すでに発表されたものでもOK。
３つ書けたら見せに来るように指示しました。
でも、ちょっと待った。式を書く前にすること。
まずノートに日付と本日のタイトル。それから図を写すこと。
私もそれを黒板に書きます。
ほどなく数人がノートを持ってやってきました。
式を説明する
式の１つを短冊黒板に書いてもらいました。
それが次々に貼られていき、黒板がごちゃごちゃしています。
そのままでは見にくいので、短冊を動かして整理をします。
重複を避けたつもりでしたが、同じものがありました。
それらをグループにして固めます。
５×２＋６＝１６
まずは、これから行こう。 この式、読めますか？
式の意味を問いました。
列指名します。
この女の子は、説明の最後に「合ってますか？」と聞いていました。
確認しているところがいいですね、とほめます。
同じように残りの式について「読んで」いきます。
式に出てくる数字は図のどこのことか？
指しながら説明をさせていきます。
出てきた式が10通り近くありました。
〔１＋１＋・・・＋１＝１６〕というのもありました。
最初に発言した子どもの数え方です。
一目で分かるものはさらりと触れて進めましたが、
その一つひとつの説明を聞くのは、ちょっと怠（だる）かったかもしれません。
転
授業を「起承転結」という言葉に当てはめれば、「転」とする時になりました。
仕掛けをしておいたのです。
その出番。
Ri-せんこれらの式に共通するのは・・・？ そう、答えの本数ですね。
この紙に書かれている棒の本数は、その16本で「当たり」でしょうか？
じゃ～ん。
と言って画用紙の折った部分を開きます。
Ri-せんあれ～、正方形のマスは７こ書かれていたのでした。
じゃあ、棒は何本でしょう？
うわー、やられた。
だまされた！
非難の嵐の中、にこにこして投げかけます。
Ri-せんもう、この式は使えませんね。
新しく考えなくてはダメなのでしょうかねぇ。
C：・・・いや。使えます。
C：そうそう、ちょっと変えればいいんだよ。
えっ、どうこうこと？
活用する
５のところを ７にすればいいんだよ。
みんなポカンとしています。
今、Aさんが言ったことが分かった人、いますか？ と尋ねても反応なし。
先生も同感。
ちょっと、何をいってるのか分かんないなぁ（と演技しつつ）、前に出て来てもらいます。
5本のところは、7本になったでしょ。
だから、この式はこうなるよ。 つまり22本です。
大いにほめます。
じゃぁ、他の式も５を７に変えれば22になるんだね？
みなさん、それでいいですか？
横の棒は7本が2列で７×２でいいけど、
縦の棒は8本になっているから＋８にしないとダメです。
Ri-せんよく気が付きましたね。他のも確かめてごらん。
時間は1分です。
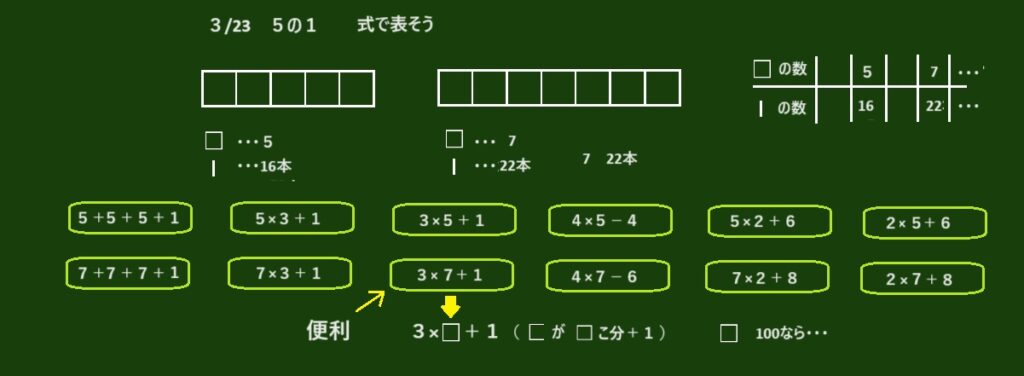
5マスから7マスに変えたときの式を言ってもらいます。
とりあえず、この４つを取り上げます。
T：どの式が便利そうですか？
C：３×７＋１の式です。
C：マスの数だけ変えればいい。
同じように投げかけます。
T：どの式が便利そうですか？
C：７×３＋１です。
C：それは、計算としては
３×７＋１と同じです。
Ri-せん３×７＋１の式は、マスの数だけ数えればいいので簡単ですね。
ということは・・・マスが9こだったら？
C：３×９＋１で本数が分かります。
C：２８本になります。
C：マスが１０こだったら本数は、３１本になるよ。
まとめ、そして発展
本数の変わり方を整理してみましょう。
どのようにするといいですか？
しーん、としているので主導していきます。
マスが１つ増えると、
棒の数はいくつ増えますか？
C：３つです。
C：コの字が１つ増えるから３本です。
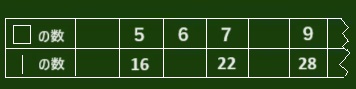
Ri-せんマスが８こなら・・・そう3本増えて25本になるね。
では問題。
マスが□こだったら、どういう式になると思う？
３×５＋１の式の５を７や９に変えたように、
そこを□にすればいいです。
Ri-せん今のBさんの発言が見えましたか？
見えた人は、ノートに書いてごらん。
［３×□＋１］です。
変わる数は、□。
３と１は変わりません。
Ri-せんこの画用紙の短冊には、正方形のマスが７つ書いてあって、
棒の本数は、22でした。誰も、当たりませんでしたね。
ところで、マスが100書いてあったら・・・棒の数はいくつでしょうね。
即座に「３０１。」と返ってきました。
これで終わりません。
もう一つ短冊を用意していました。
三角が横に並んでいます。
みなさんは、もうすぐに式がつくれますね？
書けた人は見せに来てください。
この授業の感想を言ってもらいたかったのですが、時間がきました。
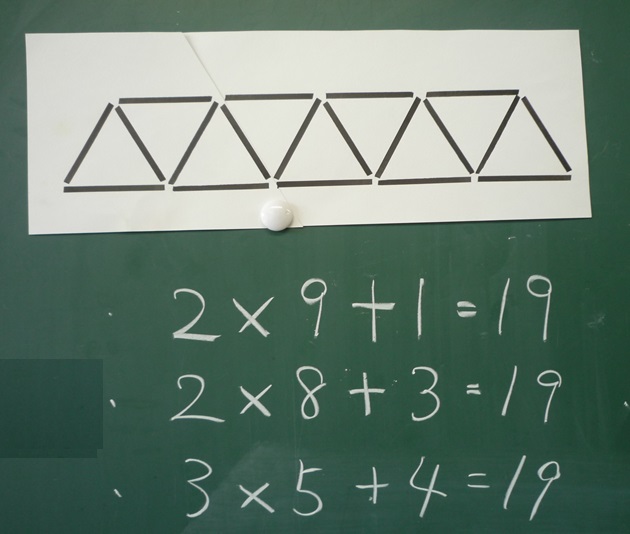
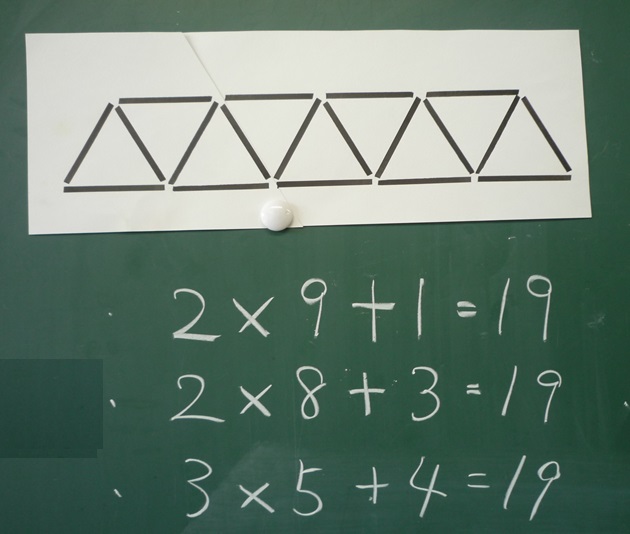
実際に行ったことを元にシナリオにしました。
その大元となっている授業があって、さる付属小学校の公開研究会でなされたものです。
追試してみたのです。
私のオリジナルでないことをお断りしておきます。
そして、授業者やパネルに登壇くださった方々に対して、多くの学びをいただいたことに感謝申し上げます。
