「引き・足し算」をご存じでしょうか。
引き算をした後に足し算をするというもので、カリキュラムにはない算数の活動です。
この計算について知ったのは、
研数学館が開催する「算数・数学講演会」でのことで、2011年～2015年の頃だったと思います。
このセミナーには足繫く通い、講師の先生方の話から多くのことを学ばせていただきました。
その中に「引き・足し算」がありました。
この記事が現場の先生方のお役に立つことがありましたら、幸いです。
研数学館のセミナーはこちら 一般財団法人 研数学館 (kensu.or.jp)
１．「引き・足し算」とは
・答えが９９になるわけ
２．自らまな板にのる （授業を公開する意図、コンセプト）
３．事前の顔合わせ （一コマ授業をさせていただく）
４．公開授業のはじまり （3文字の言葉は何だった？） → Jump there.
・難問の答え キーワードは守破離
・参観者に振ってみた
５．百玉そろばんの指導 （職員に教具を紹介する） → Jump there
６．いよいよ「引き・たし算」 （計算の手順を書く） → Jump there
・嵌（はめ）られた
７．一人の困惑を共有する （引いたら答えが一桁になって・・・）
８．３問解いたら小黒板に書かせる
９．間違いへの対応 （９９にならない！？）
・「離」への試み
１．「引き・足し算」とは
１～９の数字の中から２つ選びます。（例えば、１と６）
これで2桁の数をつくります。（16と61）
この２つの数で初めに引き算をします。
式は、61ー16。
答えは45です。
この45の位を同じように入替えると54になります。
その２つの数で足し算をします。
式は、45+54。
答えは9９になりました。
２つの計算を一つの筆算として右図のように書きます。
この計算の面白いのは、初めに選ぶ数字をいろいろと変えてみても、
答えはすべて同じで９９になることです。
９９になるわけ
答えがすべて９９になる。
そのわけは、文字式にして「引き・足し算」をするとすっきり理解できます。
選んだ２つの数をAとBとしたとき、（A＞B）
2つの数は ① 10A ＋ B と ② 10B ＋ A です。
初めに行う引き算は（ ① ー ② ）。
整理すると、（10A ーA）＋（10B ー B）＝ ９A ー 9B ＝ ９（AーB）
つまり、
答えはAとBの差の９倍ということです。
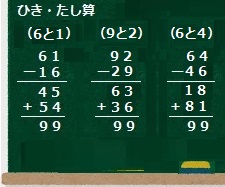
左図をごらんください。
引き算の答えである４５，６３，１８は９の倍数です。
これらは九九の「９の段」の答えです。
「９の段」の答えの数字の和は必ず９になります。
（４＋５）、（ ６＋３）、（１＋８）の答えはいずれも９です。
各位の和が９なので
「引き・足し算」の答えは、全て９９となります。
２．授業を公開する意図、コンセプト
授業を見て学ぶ。
その機会がほとんどないのが現場です。
そうした場を提供するのも、定年を迎えた教員の役目かと思いました。
範を示す、などとんでもありません。
授業づくりについて考えるきっかけになればと思いました。
自らまな板に乗った、とでも言えばいいかもしれません。
見ていただく授業行為を挙げると、次のようになります。
・授業をどのように始めるか
・板書をどうするか、小黒板をどう使うか
・百玉そろばんの指導法
・子どもとのやりとり
・授業の進め方
担任をはずれ、級外職員でした。
そこで、クラスを借りて行うことにしました。
子ども達は、思うはずです。
なぜ、僕たちのクラスに来て授業をするのだろう。
その疑問に答えるならば、
朝会等で話される講話・訓話と同じ類（たぐい）のものになります。
従って、基礎的な学力をつける時間にはなりません。
公開する授業のコンセプト（ベースとする考え方）が決まりました。
１．教科書にない内容での授業をする。
（学級担任がしている授業の続きをする訳にはいきません。）
２．事前に子ども達と顔合わせをする。
授業者（の私）は子ども達にとって、よく知らない先生です。
３．事前の顔合わせ （一コマ授業をさせていただく）
１．担任に学級をお借りすることをお願いしました。４年生です。
子ども達と顔合わせをしておきたいと考え、事前に１コマ授業しました。
算数の授業です。
自己紹介の後、
何をしているのだろうと子ども達が見ている中、図を書きました。
糸くずがからまっているような一つながりの線です。
これを赤線上で切っていったら何本になるか問いました。
答えは（ロ＋１）と表せる、という授業でした。
※これも研数学館のセミナーで学んだものです。
授業の終わりに「守・破・離」という言葉を教えました。
本来の意味を説明した後、それを学校生活につなげた話にしました。
その３文字が後日する授業のキーワードになっているとは、この時子ども達は知る由もありません。
公開に向けた準備
授業シナリオを書きました。
正にドラマのような脚本を書き、空き教室で一人模擬授業をしました。
模擬授業を始める前に、最終段階の板書を書いておきます。
授業がそこへ向かっていくように発問・指示をしていきます。
シミュレーションを何回かするうちに、板書の最終形が決まっていきます。
メモを見ながら授業をしなくても大丈夫な状態になりました。
短冊黒板や小黒板、小物類も用意します。
４．公開授業のはじまり
挨拶をしたら、さっそく投げかけます。
Ri-せん先週みなさんと勉強したとき、３文字の言葉を教えました。
何だったか、覚えていますか？
C：しゅはりぃ？
覚えている子どもがいて、思わず笑顔になりました。
前回と同じところに「守 破 離」と書き、意味をおさらいしました。
Ri-せん教えのとおりにするのが「守」。
今日の授業で「破」や「離」が起こるといいですね。
はい、全員起立！
短冊黒板を提示し、ロに入る数が分かった人は座りましょう、と指示しました。
ものの数秒で、全員座りました。
数人に当てると皆「６です」と答えます。 正解です。
問題を取り替えます。
ロに入る数が分かった人は同じように座ります。
列で言わせていくと、「３」「３」「３」・・・。
正解です。
次は難しい！
分からないと座れません。立ち続けている子ども達がいます。
自分に正直ですね、えらい！ とほめて座らせます。
２です、と答えた子に笑顔で「正解です。」と言います。
なぜ２になるのか、別な列を当て、理由をいってもらいます。
※これは、「フィボナッチ数列」です。 フィボナッチ数 – Wikipedia
キーワードは守破離
T：さあ、超難問です。 □に入る数は何でしょう。
誰も座りません。座れません。分からないのです。
ヒントがほしい、というので、
ハイフンを書き足し、黒板の端に書いておいた「守 破 離」の「離」を指しました。
これまでの問題にはきまりがありました。
そこから「離」れて考える、というサジェスチョン（示唆）です。
「ハイフン」を指さしましたが、それでもなお、子ども達は首を傾げていました。
参観者に振ってみた
参観をしている先生方に振ってみました。
Ri-せん先生方で、お分かりになった方はいらっしゃいますか？
すると、ぽっと手を挙げた職員がいます。
子ども達にきいてみます。
〇〇先生が手を挙げてますけど、聞いてみたい？
一斉に後ろを振り返る子ども達。 うん！
□に入る数字は１だと思います。
ひょっとして、学校の電話番号ではないでしょうか？
大正解。
えーっ、うっそー、何それー。
子ども達は、大騒ぎ。
その嵐の中、右端の「守 破 離」をコンコンとやって、百玉そろばんを出しました。
５．百玉そろばんの指導 （教具を紹介する）
授業で使っている教員を見たことが全くありません。
この教具を知らないのです。
数の概念形成や数の合成・分解を視覚的に捉えさせるもので、
低学年の指導には欠かせない教具だと思います。
４年生のこの学級に「１ずつ」や「２飛び」をすることは、
指導段階としてはマッチしていませんが、
声を合わせるうちに子ども達が再び集中しだしました。
気分転換を入れたわけです。
子どもが進めてもできることが伝わったと思います。
６．いよいよ「引き・たし算」 （計算の手順を書く）
ここまでの前置きが長すぎる、という指摘が出ることは織り込み済みです。
いろいろと見ていただきたい活動ではあったわけです。
百玉そろばんを片付けて仕切り直します。
これから「引き・足し算」をしましょう、と投げかけました。
まず、黒板の左端に手順を書きました。（左図）
２人を指名し、１～６までの数カードから２枚選んでもらいます。
Aさんは３と５でした。
従って、その数字でできる２桁の数は３５と５３となります。
手順の２番目。
ひき算は、５３ー３５です。 全員にノートに書くよう指示しました。
手順の3番目。
引き算の答えの「１８」は、位をひっくり返して「８１」にし、「１８」に足す、と説明。
１８+８１の計算の答えは９９になりました。
なお、この筆算形式は今回だけであることを断っておきます。
念のため、数字を変えてもう一度します。
Bさんは、数字カードの４と２を選んでいました。
先ほどの計算の隣に書いていきます。
T：この計算の仕方は分かりましたか？ ホントに？
それにしても、何かヘンですよね？
C：あれ？
選んだ数字が違うのに、答えが同じになっているよ。
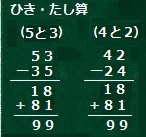
どこかから「今度は１と３でやってみて」という声がしました。
すると即座に「また９９になっちゃうよ」と返ってきました。
嵌（はめ）られた！
「１と３でやってみて！」というリクエストに応えます。
この数で「引き・足し算」をしても９９になるのでしょうか。
やってみなくちゃわからない
と子ども達。やってみます。 ３１－１３＝１８
その後は、前の計算と同じなので答えは９９です。
えーっ！ すげぇ！ なんで？ どーなってるの？
子ども達の言葉を拾って黒板に書いていきます。
Ri-せんたまたまですよねー、こんなことは。 誰か別な数を選んでみる？
わーっと手が挙がりました。
６と２が選ばれたとたん、自ら計算を始める子ども達。
やはり９９になりました。
ふと疑問が湧いたようでした。
嵌（はめ）められた！ というのです。
どういう事なの？ と問うと・・・・
数字カードが６までしかない、というのです。
では、どうしたいの？
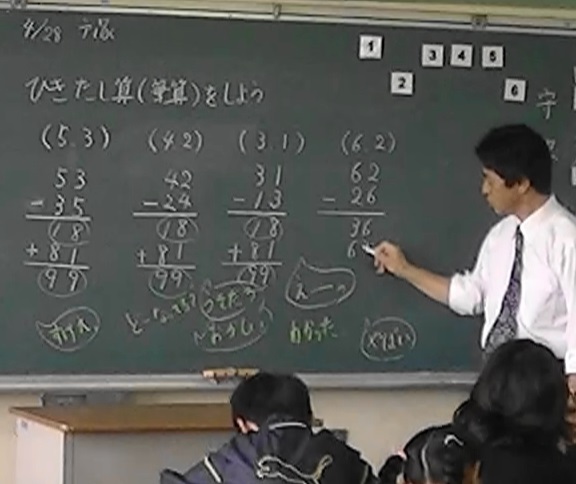
子どもカードが６までしかないから、７とか８とか０も使ってみたいんだけど。
面白くなってきました。（想定通りですが。）
「そう言うだろうと思ってね・・・」と言いつつ左ポケットから７，８、９を出して並べました。
T：これでもう、答えが９９になることは起こらないよね？
反応は、分かれました。
「９９にならない事もある」という子ども達は少数派で、6,7人。
残りは「同じように９９になる」で多数でした。
各自で確かめるよう指示。
任意で数字を選んで「引き・足し算」を3つしたら終了です。
７．困惑を共有する （引いたら答えが一桁になって・・・）
手が止まっている子どもに気が付きました。
ノートを見ると・・・
ひき算の答えが1桁になって、先へ進めなくなっていました。
たし算をしようにも、たす数が分からないようでした。
さっそく全体にストップをかけます。
「」
Ri-せん計算中、ちょっと、ゴメン。 鉛筆を置いてください。
Dさんが９８－８９で引き算したら答えが９になって、今
困っているんです。
数字の入替えをしてたし算をつくることができません。
どうしたらいいか投げかけました。
「９０にすればいい」という発言がありました。
「ああ、そうか」という声も聞こえたので、困惑していたのは、他にも居たようです。
解決したので、続きをするよう促しました。
自分で３問つくり、し終えたら気が付いたこと（感想）を書くようにと指示しました。
８．小黒板に書かせる
子どもがノートを持って見せにきました。
３問やり終えたのです。（右図）
その中の１つを小黒板に書くように指示しました。
小黒板というのは、手作りの教具（私物）です。
大きさは、６０×４５cm。
DIYでべニア板を買ってきて、黒板塗料を塗って作りました。
小黒板は、この後黒板に張り付けていきます。
数字を２つ選んで出来る２桁の数は、何十通りもあり、
すべての場合を確かめる事はできません。
そこで、
いくつかの例を挙げてみようというわけです。
小黒板に書かせる指示は、「空白対策」の一つでもあります。
空白とは、課題を終えた子どもが何もすることが無くなっている時間のことです。
手際のよい、いわゆる「賢い子ども」が無為に過ごしてしまいます。
それをできるだけ取り除きたいわけです。
感想を書かせるのもその一つです。
９．間違いへの対応 （９９にならない！？）
小黒板に書かせた計算は、８通りでストップさせました。
重複のないようにしてあります。
これより、
個々の取組みを、全体で共有していきます。
１枚目から貼っていきます。
１つずつ貼るのは、１つずつ注目させるためです。
まず鉛筆を置かせます。
そして、小黒板を１枚ずつ見せていきます。
７枚目を一番左に貼りました。
答えが、なんと８８になっています。
T：Oh！９９にならないのがありました！
やりましたねー！！
実は、これは計算のミスでした。
初めの引き算で間違っていました。
他の子どもがその指摘をします。
ここは、教師の出番です。
当該の子どもは恥ずかしい思いをしているはずです。
その小黒板を出す時に、配慮ができたはずですが、後の祭りでした。
全力でフォローしなくてはいけません。
Ri-せん間違えない人はいません。誰でも間違いはします。
先生も、いっぱい間違いをしてきましたし、これからもするでしょう。
間違えると恥ずかしい思いをしますが、学ぶことができます。
この場合は、確かめることが大切、ということかな。
そこに気づかせてもらいました。Bさん、間違えてくれてありがとう。
小黒板８枚の計算結果は、すべて９９になりました。
９９以外の計算結果になったという子どもはいませんでした。
１０．まとめへ （「離」への試み）
授業は終盤。
まとめにはいります。
黒板の右端に書いた「守・破・離の『守』」を指しながら投げかけました。
T：今日は「引き・足し算」をしました。
皆さんは、計算の仕方に従って答えを出しました。
答えは、すべて９９になりましたね。
ところで・・・
今日の授業で、「守破離」の「破」はありましたか？
あった、と言ってくれました。
初め１～６しかなかったところに７，８，９，０をつけ
たして計算してみた、と返ってきました。
これは、「破」と言っていいかもしれません。
Ri-せんでは、「守破離の『離』は、ありましたか？ 今考えてもいいですよ。
子ども達からは、何の反応もありませんでした。
期待したのは、３桁の数にしてみるという考え方でした。
右図のように
数を６，３，２と選び、
それを使って「引き・足し算」をすると1089になります。
数字を変えて計算してもやはり、1089になります。
これをさらに発展させると
4桁以降はどのような答えになるかという話になっていきます。
あるいは、
順序を逆にして「引き・足し算」ではなく、
「足し・ひき算」という計算でしてみる、でもよかったかもしれません。
授業は、３分伸びてしまいました。
関連記事
